#INTERVAL OF CONVERGENCE COMPARISON TEST

[bugmistake]

literally longing for calc 1 like i'm an old woman looking at a heart shaped locket with a picture of an old lover from my youth.. please god bring me back to those days..... please just let me do derivatives and l'hopital's rule again.... (coughing blood into a handkerchief) chain rule.. please. .

[foxspain82]

10.4 Usubstitution Trig Functionsap Calculus

10.4 U-substitution Trig Functionsap Calculus Answers

10.4 U-substitution Trig Functionsap Calculus Pdf

10.4 U-substitution Trig Functionsap Calculus Problems

10.4 U-substitution Trig Functionsap Calculus Worksheet

Calculus II, Section 7.4, #67 Integration of Rational Functions by Partial Fractions One method of slowing the growth of an insect population without the use of pesticides is to introduce into the population a number of sterile males that mate with fertile females but produce no o spring. Let P represeent. AP Calculus AB Mu Alpha Theta Welcome to AP Calculus AB! Contact me here. Need more review? Browse the Algebra II and Pre-Calculus Tabs. AP ® Calculus AB and BC. COURSE AND EXAM DESCRIPTION. AP COURSE AND EXAM DESCRIPTIONS ARE UPDATED PERIODICALLY. Please visit AP Central. Mathematics 104—Calculus, Part I (4h, 1 CU) Course Description: Brief review of High School Calculus, methods and applications of integration, infinite series, Taylor's theorem, first order ordinary differential equations. Use of symbolic manipulation and graphics software in Calculus. Note: This course uses Maple®.

Math 104: Calculus I – Notes

Section 004 - Spring 2014

10.4 U-substitution Trig Functionsap Calculus Answers

Syllabus

Concept Videos

Skeleton NotesComplete Notes Title More Remainder 10.6, 10.9 Remainder 10.6/10.9 Series Estimation & Remainder Sections 10.8-10.10 Sections 10.8-10.10 Taylor (and Maclaurin) Series Section 10.7 Section 10.7 Power Series Introduction Section 10.6 Section 10.6 Alt. Series Test and Abs. Conv. Conv. Tests Section 10.5 Section 10.5 The Ratio and Root Tests Section 10.4 Section 10.4 The Comparison Tests Section 10.3 Section 10.3 The Integral Test Section 10.2 Section 10.2 Introduction to Series Section 10.1 Section 10.1 Sequences Section 9.2 Section 9.2 Linear Differential Equations Section 7.2 Pt 1Pt 2 Section 7.2 Separable Differential Equations Section 8.8 Section 8.8 Probability and Calculus Odd Ans. Section 8.7 Pt. 1Pt. 2Section 8.7 Improper Integrals L'Hopital Section 8.4 Pt. 1Pt. 2Section 8.4 Partial Fraction Decomposition Section 8.3 Pt. 1Pt. 2Section 8.3 Trig. Substitution Section 8.2 Pt. 1Pt. 2Section 8.2 Integrating Trig. Powers Section 8.1 Pt. 1Pt. 2 Section 8.1 Integration By Parts Section 6.6 Section 6.6 Center of Mass Section 6.4 Section 6.4 Surface Area of Revolution Section 6.3 Section 6.3 Arc Length Section 6.2Section 6.2 Volumes Using Cylindrical Shells Section 6.1 Section 6.1 Volumes Using Cross-Sections disk/washer Review Calc I Review Calc I ReviewLimit, Derivative, and Integral Area b/w CurvesArea b/w Curves Video Example U-substitution Graphs you should know

Print out the skeleton notes before class and bring them to class so that you don't have to write down https://foxspain82.tumblr.com/post/657282647494672384/achievement-unlocked-2watermelon-gaming. Hide paragraph marks in microsoft word for mac. everything said in class. If you miss anything, the complete notes will be posted after class.

10.4 U-substitution Trig Functionsap Calculus Pdf

My Penn Page | Penn Math 104 Page| Penn Undergraduate Math | Advice | Help|

10.4 U-substitution Trig Functionsap Calculus Problems

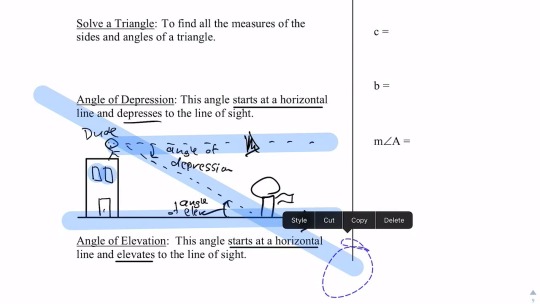
10.4 U-substitution Trig Functionsap Calculus Worksheet

Version #1 ​The course below follows CollegeBoard's Course and Exam Description. Lessons will begin to appear starting summer 2020. BC Topics are listed, but there will be no lessons available for SY 2020-2021

Unit 0 - Calc Prerequisites (Summer Work) 0.1 Summer Packet

Unit 1 - Limits and Continuity 1.1 Can Change Occur at an Instant? 1.2 Defining Limits and Using Limit Notation 1.3 Estimating Limit Values from Graphs 1.4 Estimating Limit Values from Tables 1.5 Determining Limits Using Algebraic Properties (1.5 includes piecewise functions involving limits) 1.6 Determining Limits Using Algebraic Manipulation 1.7 Selecting Procedures for Determining Limits (1.7 includes rationalization, complex fractions, and absolute value) 1.8 Determining Limits Using the Squeeze Theorem 1.9 Connecting Multiple Representations of Limits Mid-Unit Review - Unit 1 1.10 Exploring Types of Discontinuities 1.11 Defining Continuity at a Point 1.12 Confirming Continuity Over an Interval 1.13 Removing Discontinuities 1.14 Infinite Limits and Vertical Asymptotes 1.15 Limits at Infinity and Horizontal Asymptotes 1.16 Intermediate Value Theorem (IVT) Review - Unit 1

Unit 2 - Differentiation: Definition and Fundamental Properties 2.1 Defining Average and Instantaneous Rate of Change at a Point 2.2 Defining the Derivative of a Function and Using Derivative Notation (2.2 includes equation of the tangent line) 2.3 Estimating Derivatives of a Function at a Point 2.4 Connecting Differentiability and Continuity 2.5 Applying the Power Rule 2.6 Derivative Rules: Constant, Sum, Difference, and Constant Multiple (2.6 includes horizontal tangent lines, equation of the normal line, and differentiability of piecewise) 2.7 Derivatives of cos(x), sin(x), e^x, and ln(x) 2.8 The Product Rule 2.9 The Quotient Rule 2.10 Derivatives of tan(x), cot(x), sec(x), and csc(x) Review - Unit 2

Unit 3 - Differentiation: Composite, Implicit, and Inverse Functions 3.1 The Chain Rule 3.2 Implicit Differentiation 3.3 Differentiating Inverse Functions 3.4 Differentiating Inverse Trigonometric Functions 3.5 Selecting Procedures for Calculating Derivatives 3.6 Calculating Higher-Order Derivatives Review - Unit 3

Unit 4 - Contextual Applications of Differentiation 4.1 Interpreting the Meaning of the Derivative in Context 4.2 Straight-Line Motion: Connecting Position, Velocity, and Acceleration 4.3 Rates of Change in Applied Contexts Other Than Motion 4.4 Introduction to Related Rates 4.5 Solving Related Rates Problems 4.6 Approximating Values of a Function Using Local Linearity and Linearization 4.7 Using L'Hopital's Rule for Determining Limits of Indeterminate Forms Review - Unit 4

Unit 5 - Analytical Applications of Differentiation 5.1 Using the Mean Value Theorem 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points 5.3 Determining Intervals on Which a Function is Increasing or Decreasing 5.4 Using the First Derivative Test to Determine Relative Local Extrema 5.5 Using the Candidates Test to Determine Absolute (Global) Extrema 5.6 Determining Concavity of Functions over Their Domains 5.7 Using the Second Derivative Test to Determine Extrema Mid-Unit Review - Unit 5 5.8 Sketching Graphs of Functions and Their Derivatives 5.9 Connecting a Function, Its First Derivative, and Its Second Derivative (5.9 includes a revisit of particle motion and determining if a particle is speeding up/down.) 5.10 Introduction to Optimization Problems 5.11 Solving Optimization Problems 5.12 Exploring Behaviors of Implicit Relations Review - Unit 5

Unit 6 - Integration and Accumulation of Change 6.1 Exploring Accumulation of Change 6.2 Approximating Areas with Riemann Sums 6.3 Riemann Sums, Summation Notation, and Definite Integral Notation 6.4 The Fundamental Theorem of Calculus and Accumulation Functions 6.5 Interpreting the Behavior of Accumulation Functions ​ Involving Area Mid-Unit Review - Unit 6 6.6 Applying Properties of Definite Integrals 6.7 The Fundamental Theorem of Calculus and Definite Integrals 6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation 6.9 Integrating Using Substitution 6.10 Integrating Functions Using Long Division ​ and Completing the Square 6.11 Integrating Using Integration by Parts (BC topic) 6.12 Integrating Using Linear Partial Fractions (BC topic) 6.13 Evaluating Improper Integrals (BC topic) 6.14 Selecting Techniques for Antidifferentiation Review - Unit 6

Unit 7 - Differential Equations 7.1 Modeling Situations with Differential Equations 7.2 Verifying Solutions for Differential Equations 7.3 Sketching Slope Fields 7.4 Reasoning Using Slope Fields 7.5 Euler's Method (BC topic) 7.6 General Solutions Using Separation of Variables 7.7 Particular Solutions using Initial Conditions and Separation of Variables 7.8 Exponential Models with Differential Equations 7.9 Logistic Models with Differential Equations (BC topic) Review - Unit 7

Unit 8 - Applications of Integration 8.1 Average Value of a Function on an Interval 8.2 Position, Velocity, and Acceleration Using Integrals 8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts 8.4 Area Between Curves (with respect to x) 8.5 Area Between Curves (with respect to y) 8.6 Area Between Curves - More than Two Intersections Mid-Unit Review - Unit 8 8.7 Cross Sections: Squares and Rectangles 8.8 Cross Sections: Triangles and Semicircles 8.9 Disc Method: Revolving Around the x- or y- Axis 8.10 Disc Method: Revolving Around Other Axes 8.11 Washer Method: Revolving Around the x- or y- Axis 8.12 Washer Method: Revolving Around Other Axes 8.13 The Arc Length of a Smooth, Planar Curve and Distance Traveled (BC topic) Review - Unit 8

Unit 9 - Parametric Equations, Polar Coordinates, and Vector-Valued Functions (BC topics) 9.1 Defining and Differentiating Parametric Equations 9.2 Second Derivatives of Parametric Equations 9.3 Arc Lengths of Curves (Parametric Equations) 9.4 Defining and Differentiating Vector-Valued Functions 9.5 Integrating Vector-Valued Functions 9.6 Solving Motion Problems Using Parametric and Vector-Valued Functions 9.7 Defining Polar Coordinates and Differentiating in Polar Form 9.8 Find the Area of a Polar Region or the Area Bounded by a Single Polar Curve 9.9 Finding the Area of the Region Bounded by Two Polar Curves Review - Unit 9

Unit 10 - Infinite Sequences and Series (BC topics) 10.1 Defining Convergent and Divergent Infinite Series 10.2 Working with Geometric Series 10.3 The nth Term Test for Divergence 10.4 Integral Test for Convergence 10.5 Harmonic Series and p-Series 10.6 Comparison Tests for Convergence 10.7 Alternating Series Test for Convergence 10.8 Ratio Test for Convergence 10.9 Determining Absolute or Conditional Convergence 10.10 Alternating Series Error Bound 10.11 Finding Taylor Polynomial Approximations of Functions 10.12 Lagrange Error Bound 10.13 Radius and Interval of Convergence of Power Series 10.14 Finding Taylor Maclaurin Series for a Function 10.15 Representing Functions as a Power Series Review - Unit 8

Version #2 ​The course below covers all topics for the AP Calculus AB exam, but was built for a 90-minute class that meets every other day. Lessons and packets are longer because they cover more material.

Unit 0 - Calc Prerequisites (Summer Work) 0.1 Things to Know for Calc 0.2 Summer Packet 0.3 Calculator Skillz

Unit 1 - Limits 1.1 Limits Graphically 1.2 Limits Analytically 1.3 Asymptotes 1.4 Continuity Review - Unit 1

Unit 2 - The Derivative 2.1 Average Rate of Change 2.2 Definition of the Derivative 2.3 Differentiability (Calculator Required) ​ Review - Unit 2

Unit 3 - Basic Differentiation 3.1 Power Rule 3.2 Product and Quotient Rules 3.3 Velocity and other Rates of Change 3.4 Chain Rule 3.5 Trig Derivatives Review - Unit 3

Unit 4 - More Deriviatvies 4.1 Derivatives of Exp. and Logs 4.2 Inverse Trig Derivatives 4.3 L'Hopital's Rule Review - Unit 4

Unit 5 - Curve Sketching 5.1 Extrema on an Interval 5.2 First Derivative Test 5.3 Second Derivative Test Review - Unit 5

Unit 6 - Implicit Differentiation 6.1 Implicit Differentiation 6.2 Related Rates 6.3 Optimization ​ Review - Unit 6

Unit 7 - Approximation Methods 7.1 Rectangular Approximation Method 7.2 Trapezoidal Approximation Method Review - Unit 7

Unit 8 - Integration 8.1 Definite Integral 8.2 Fundamental Theorem of Calculus (part 1) 8.3 Antiderivatives (and specific solutions) Review - Unit 8

Unit 9 - The 2nd Fundamental Theorem of Calculus 9.1 The 2nd FTC 9.2 Trig Integrals 9.3 Average Value (of a function) 9.4 Net Change Review - Unit 9

Unit 10 - More Integrals 10.1 Slope Fields 10.2 u-Substitution (indefinite integrals) 10.3 u-Substitution (definite integrals) 10.4 Separation of Variables Review - Unit 10

Unit 11 - Area and Volume 11.1 Area Between Two Curves 11.2 Volume - Disc Method 11.3 Volume - Washer Method ​ 11.4 Perpendicular Cross Sections Review - Unit 11

[mamtajuyal1986]

IIT JAM 2020 Mathematics (MA) Syllabus | IIT JAM 2020 Mathematics (MA) Exam Pattern

IIT JAM 2020 Mathematics (MA) Syllabus | IIT JAM 2020 Mathematics (MA) Exam Pattern Mathematics (MA): The syllabus is a very important aspect while preparing for the examination. Therefore it is advised to all the appearing candidates that they should go through the Mathematics (MA) syllabus properly before preparing for the examination. Sequences and Series of Real Numbers: Sequence of real numbers, convergence of sequences, bounded and monotone sequences, convergence criteria for sequences of real numbers, Cauchy sequences,subsequences, Bolzano-Weierstrass theorem. Series of real numbers, absolute convergence, tests of convergence for series of positive terms - comparison test, ratio test, root test; Leibniz test for convergence of alternating series. Functions of One Real Variable: Limit, continuity, intermediate value property, differentiation, Rolle's Theorem, mean value theorem, L'Hospital rule, Taylor's theorem, maxima and minima. Functions of Two or Three Real Variables: Limit, continuity, partial derivatives, differentiability, maxima and minima. Integral Calculus: Integration as the inverse process of differentiation, definite integrals and their properties, fundamental theorem of calculus. Double and triple integrals, change of order of integration, calculating surface areas and volumes using double integrals, calculating volumes using triple integrals. Differential Equations: Ordinary differential equations of the first order of the form y'=f(x,y), Bernoulli,s equation, exact differential equations, integrating factor, orthogonal trajectories, homogeneous differential equations, variable separable equations, linear differential equations of second order with constant coefficients, method of variation of parameters, Cauchy-Euler equation. Vector Calculus: Scalar and vector fields, gradient, divergence, curl, line integrals, surface integrals, Green, Stokes and Gauss theorems. Group Theory: Groups, subgroups, Abelian groups, non-Abelian groups, cyclic groups, permutation groups, normal subgroups, Lagrange's Theorem for finite groups, group homomorphisms and basic concepts of quotient groups. Linear Algebra: Finite dimensional vector spaces, linear independence of vectors, basis, dimension, linear transformations, matrix representation, range space, null space, rank-nullity theorem. Rank and inverse of a matrix,determinant, solutions of systems of linear equations, consistency conditions, eigenvalues and eigenvectors for matrices,Cayley-Hamilton theorem. Real Analysis: Interior points, limit points, open sets, closed sets, bounded sets, connected sets, compact sets, completeness of R. Power series (of real variable), Taylor,s series, radius and interval of convergence, term-wise differentiation and integration of power series. Related Articles: IIT JAM 2020 Syllabus Biotechnology (BT) Syllabus Biological Sciences (BL) Syllabus Chemistry (CY) Syllabus Geology (GG) Syllabus Mathematics (MA) Syllabus Mathematical Statistics (MS) Syllabus Physics (PH) Syllabus Read the full article

[cancersfakianakis1]

Test-retest reliability and convergent validity of (R)-[ 11 C]PK11195 outcome measures without arterial input function

Abstract

Purpose

The PET radioligand (R)-[11C]PK11195 is used to quantify the 18-kDa translocator protein (TSPO), a marker for glial activation. Since there is no brain region devoid of TSPO, an arterial input function (AIF) is ideally required for quantification of binding. However, obtaining an AIF is experimentally demanding, is sometimes uncomfortable for participants, and can introduce additional measurement error during quantification. The objective of this study was to perform an evaluation of the test-retest reliability and convergent validity of techniques used for quantifying (R)-[11C]PK11195 binding without an AIF in clinical studies.

Methods

Data from six healthy individuals who participated in two PET examinations, 6 weeks apart, were analyzed. Regional non-displaceable binding potential (BPND) values were calculated using the simplified reference tissue model, with either cerebellum as reference region or a reference input derived using supervised cluster analysis (SVCA). Standardized uptake values (SUVs) were estimated for the time interval of 40–60 min.

Results

Test-retest reliability for BPND estimates were poor (80% of ICCs < 0.5). BPND estimates derived without an AIF were not correlated with BPND, total or specific distribution volume from the 2TCM using an AIF (all R2 < 12%). SUVs showed moderate reliability but no correlation to any other outcome measure.

Conclusions

Caution is warranted when interpreting patient-control comparisons employing (R)-[11C]PK11195 outcome measures obtained without an AIF.

https://ift.tt/2FPFNeF

[mamtajuyal1986]

IIT JAM 2020 Mathematical Statistics (MS) Syllabus | IIT JAM 2020 Mathematical Statistics (MS) Exam Pattern

IIT JAM 2020 Mathematical Statistics (MS) Syllabus | IIT JAM 2020 Mathematical Statistics (MS) Exam Pattern Mathematical Statistics (MS): The syllabus is a very important aspect while preparing for the examination. Therefore it is advised to all the appearing candidates that they should go through the Mathematical Statistics (MS) syllabus properly before preparing for the examination. The Mathematical Statistics (MS) test paper comprises of Mathematics (40% weightage) and Statistics (60%weightage). MATHEMATICS Sequences and Series: Convergence of sequences of real numbers, Comparison, root and ratio tests for convergence of series of real numbers. Differential Calculus: Limits, continuity and differentiability of functions of one and two variables. Rolle's theorem, mean value theorems, Taylor's theorem, indeterminate forms, maxima and minima of functions of one and two variables. Integral Calculus: Fundamental theorems of integral calculus. Double and triple integrals, applications of definite integrals, arc lengths, areas and volumes. Matrices: Rank, inverse of a matrix. Systems of linear equations. Linear transformations, eigenvalues and eigenvectors. Cayley-Hamilton theorem, symmetric, skew-symmetric and orthogonal matrices. STATISTICS Probability: Axiomatic definition of probability and properties, conditional probability, multiplication rule. Theorem of total probability. Bayes' theorem and independence of events. Random Variables: Probability mass function, probability density function and cumulative distribution functions, distribution of a function of a random variable. Mathematical expectation, moments and moment generating function. Chebyshev's inequality. Standard Distributions: Binomial, negative binomial, geometric, Poisson, hypergeometric, uniform, exponential, gamma, beta and normal distributions. Poisson and normal approximations of a binomial distribution. Joint Distributions: Joint, marginal and conditional distributions. Distribution of functions of random variables. Joint moment generating function. Product moments, correlation, simple linear regression. Independence of random variables. Sampling Distributions: Chi-square, t and F distributions, and their properties. Limit Theorems: Weak law of large numbers. Central limit theorem (i.i.d.with finite variance case only). Estimation: Unbiasedness, consistency and efficiency of estimators, method of moments and method of maximum likelihood. Sufficiency, factorization theorem. Completeness, Rao-Blackwell and Lehmann-Scheffe theorems, uniformly minimum variance unbiased estimators. Rao-Cramer inequality. Confidence intervals for the parameters of univariate normal, two independent normal, and one parameter exponential distributions. Testing of Hypotheses: Basic concepts, applications of Neyman-Pearson Lemma for testing simple and composite hypotheses. Likelihood ratio tests for parameters of univariate normal distribution. Related Articles: IIT JAM 2020 Syllabus Biotechnology (BT) Syllabus Biological Sciences (BL) Syllabus Chemistry (CY) Syllabus Geology (GG) Syllabus Mathematics (MA) Syllabus Mathematical Statistics (MS) Syllabus Physics (PH) Syllabus Read the full article